MINDOMO (Módulo III)

MAPA SEMÁNTICO

Son una estructuración categórica de la información o diagramas que ayudan a ver como se relacionan las palabras entre sí y activan el conocimiento previo.

Son utilizados en el aula especialmente en actividades de aprendizaje y repaso. Esta estrategia visual fue descrita inicialmente por Pearson y Johnson (1978).

Situaciones de uso contextualizado:
Área: Matemática Nivel Secundaria

1. Puedo utilizar esta herramienta como una valiosa técnica al inicio de la sesión de aprendizaje para explorar los conocimientos previos de los estudiantes, además que es muy motivadora.
2. También lo puedo utilizar para organizar e integrar la información previo a una situación de análisis hecha por los estudiantes, permitiendo al mismo tiempo comprobar el avance o logro de la capacidad indicada.

¿Que es mindomo?

Mindomo es una herramienta web para la creación de mapas de forma gratuita y sencilla en línea que permite introducir toda clase de contenido, ya sea texto, hiperenlaces, vídeos, música e imágenes.

Tenemos la posibilidad de exportar un mapa, en cualquiera de los siguientes formatos: Imagen, Archivo de texto sin formato, RTF(tipo microsoft word) y PDF.

Permite además compartir nuestro mapa con otras vía internet y es muy útil para principiantes ya que no se requiere conocimiento del lenguaje HTML.

Se puede utilizar la herramienta directamente desde internet, no es necesario descargar un software específico para su uso.

Puedes registrarte ingresando a la siguiente dirección: https://www.mindomo.com/es/

Make your own mind maps with Mindomo.

TEXTO UTILIZADO PARA LA ELABORACIÓN DEL MAPA SEMÁNTICO

TEMA: Ángulos ÁREA: Matemáticas
GRADO: 1ro NIVEL: Secundaria

TRIÁNGULOS

La suma de los ángulos interiores de cualquier triángulo es 180º

Triángulo ABC: Tiene tres lados: AB, BC, CA

Tiene tres vértices: A, B, C

Tiene tres ángulos: ∠ ABC, ∠ BCA, ∠ CAB

Clasificación de los triángulos

Los triángulos se pueden clasificar según:

Las medidas de sus lados

Las medidas de sus ángulos

Según las medidas de sus lados pueden ser, triángulo:

Equilátero

Isósceles

Escaleno

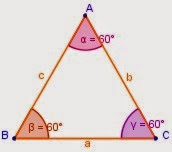
Triángulo equilátero: Es el que tiene sus tres lados de igual medida y sus tres ángulos de igual medida, cada uno de los cuales mide 60º.

Los lados a, b y c tienen igual medida.

Esto se puede escribir también de la siguiente manera:

AB = BC = CA
Los ángulos tienen igual medida, es decir:

∠ ABC = ∠ BCA = ∠ CAB = 60º

Recuerda que siempre la letra que está en el medio indica el vértice donde se ubica el ángulo.

Triángulo isósceles: Es el que tiene dos lados de igual medida, por lo tanto, tiene dos ángulos de igual medida.

trazo AB = trazo AC

∠ ABC = ∠ BCA

Triángulo escaleno: Es el que tiene todos sus lados de distinta medida y, por lo tanto, sus ángulos también son de distinta medida.

Según la medida de sus ángulos, un triángulo puede ser:

Triángulo acutángulo: Es el que tiene sus tres ángulos agudos; es decir, sus ángulos miden más de 0º y menos de 90º. tal como se muestra en la imagen.